What do you think of when you hear the word “mathematics?”

For me, it’s a lot of indecipherable scribbles that my teacher wrote on the board in high school algebra class. In my head, math is something you have to endure until you get to more interesting subjects. But what if I told you that math is used in architecture, and that if you’re an architect, you’ll probably be using those formulas every day?

Sure, there are parts of architecture design that don’t require much math. You can draw up floor plans and blueprints by hand and watch your ideas come to life. But what happens when your client comes back with a request for a new set of blueprints? Do you want to redraw everything from scratch, or would you rather use a few simple formulas to scale up or down your existing plans?

If you’re like most architects out there, you’ll choose the latter.

Every building you spend time in––schools, libraries, houses, apartment complexes, movie theaters, and even your favorite ice cream shop––is the product of mathematical principles applied to design and construction. Have you ever wondered how building professionals incorporate math to create the common structures you walk in and out of every day?

Before construction workers can build a habitable structure, an architect has to design it. Geometry, algebra, and trigonometry all play a crucial role in architectural design. Architects apply these math forms to plan their blueprints or initial sketch designs. They also calculate the probability of issues the construction team could run into as they bring the design vision to life in three dimensions.

Since ancient times, architects have used geometric principles to plan the shapes and spatial forms of buildings. In 300 B.C., the Greek mathematician Euclid defined a mathematical law of nature called the Golden Ratio. For more than two thousand years, architects have used this formula to design proportions in buildings that look pleasing to the human eye and feel balanced. It is also known as the Golden Constant because it manifests literally everywhere.

The Golden Ratio still serves as a basic geometric principle in architecture. You could even call it a timeless archetype, as it evokes in human beings a universal sense of harmony when they see or stand in a building designed with this principle. And perhaps not surprisingly, we see the Golden Ratio demonstrated throughout “architectures” of the natural world. Read here to learn more!

Calculating ratio is essential, as well, when it’s time to construct a building from the architectural blueprints. For example, it’s important to get the proportions right between the height and length of a roof. To do that, building professionals divide the length by the height to get the correct ratio.

The Pythagorean theorem, formulated in the 6th century B.C., has also come into play for centuries to calculate the size and shape of a structure. This theorem enables builders to accurately measure right angles. It states that in a triangle the square of the hypotenuse (the long side opposite the right angle) is equal to the sum of the squares of the other two sides. Read here to find out more about how builders use the Pythagorean theorem to make roofs!

The most remarkable ancient architecture of all may be the pyramids of Egypt, constructed between 2700 B.C. and 1700 B.C. Most of them were built and scaled at about a 51-degree angle. The Egyptians clearly and mysteriously possessed knowledge of geometry, as evidenced by the accuracy of pyramid construction. Just in case you’re curious about the geometry and triangle mathematics that ancient Egyptians applied to build their pyramids, read here.

In the modern world, builders use math every day to do their work. Construction workers add, subtract, divide, multiply, and work with fractions. They measure the area, volume, length, and width. How much steel do they need for an office building? How much weight in books and furniture will the library floors need to bear? Even building a small single-family home calls for careful calculations of square footage, wall angles, roofs, and room sizes. How many square yards of carpet? How much water do you need to fill up a swimming pool?

Chances are you’re in a building right now. Look around at the walls and windows. Math is everyplace you walk into––work, school, home, or pet store. Imagine that you are an architect. How would you apply math to build a small dwelling?

Read on to know more about Math Formulas Used In Architecture, is math in architecture hard, importance of mathematics in architecture, geometry in architecture and much more here on collegelearners.

is math in architecture hard

In general, the math required for architecture is not that difficult. You’ll need to do things like addition and multiplication, as well as constructing and solving equations; you won’t need to pass an advanced calculus exam to work in the profession. Unless you really have trouble with basic calculations and logic, with a bit of hard work you’ll be fine.

You don’t have to love math to be an architect, nor do you have to be good at it. While math is necessary for the awe-inspiring buildings that define our world, in your day-to-day work as an architect you won’t be required to perform complex mathematical tasks. Even if you hate math or think of yourself as a “bad” mathematician, you can still become a successful architect.

The basics of mathematics are all that’s required for this career. It’s true that the most awe-inspiring buildings rely on mathematical concepts like geometry, but there’s no need to be a math prodigy in order to build one yourself. Instead, the most important thing is that you’re able to communicate your ideas to contractors and builders – and in order to do this, you’ll only need the basics.

As long as you put in the time and effort to master these foundational skills, you’re well on your way to becoming an architect. With practice, there’s nothing standing between you and an architecture degree!

One thing is for sure: lukewarm feelings about math shouldn’t put you off a career in architecture. There are so many skills required for architecture you’re bound to be stronger in some areas and weaker in others. Instead of losing sleep over long division, try thinking about the buildings you love most in mathematical terms – and who knows, you might even come to enjoy it.

Math Formulas Used In Architecture

Sikkim architecture mathematics

We study the 3‐D variation of the crustal structure of the Sikkim Himalaya using broadband seismological data acquired from a focused network of seven stations spanning the Lesser, Higher, and Tethyan Himalaya. Common conversion point stacking of receiver functions recorded along an across‐strike profile of the Himalaya reveals first‐order northward dip on the Main Himalayan Thrust (MHT), a midcrustal discontinuity and the Moho, along with higher‐order lateral variations. Three‐dimensional images generated from joint inversion of receiver functions and surface wave dispersions show that the MHT has a ramp‐flat‐ramp geometry. The ramps are located beneath the Lesser Himalaya and the Tethyan Himalaya with dips of ∼7∘ and ∼15∘, respectively, connected by flat segments. The ramp beneath the Lesser Himalaya forms a dome structure, upwarping the thrust sheets associated with the Peling and Main Central Thrust.

The erosional surface of this dome forms the arcuate geometry of thrusts observed in the Lesser Himalaya. The thickness of the underthrust Indian crust is 35–42 km and has an average VS of 3.63 km/s, similar to that of the Indian Shield crust. The Moho also has dome‐like structures separated by elongated, deeper sections trending NW‐SE. These are intersected by steeply dipping transverse low‐velocity zones, oblique to the strike of the Himalaya. We conjecture that these low‐velocity zones are the dextral‐strike slip faults known to be active beneath the Sikkim Himalaya. The observed alternate shallow and deep segments of the Moho must be a consequence of several cycles of strike‐slip displacement on these transverse faults.

Plain Language Summary
Sikkim is an Indian state between Nepal and Bhutan. The style of convergence between India and Eurasia changes from head‐on collision (Nepal Himalaya) to oblique convergence (Eastern Himalaya) across this region (Sikkim Himalaya). We study the crustal structure of this region using broadband seismological data recorded by a local network of stations. The Main Himalayan Thrust (MHT) separates the downgoing Indian Plate from the overriding Himalayan wedge. The MHT and the other major discontinuities within the crust, viz., the Moho and the midcrustal discontinuity are seen to dip northward. But all of these discontinuities also have higher‐order lateral variations.

The MHT has a ramp‐flat‐ramp geometry with two ramps in the Lesser Himalaya and the Tethyan Himalaya, respectively. The ramp in the Lesser Himalaya is like a dome and upwarps the overlying thrust faults. The thickness and average shear wave velocity of underthrusting Indian crust is very similar to that of the Peninsular Indian crust. The Moho also has dome‐like structure separated by elongated, deeper sections trending NW‐SE. We conjecture that these alternate shallow and deep segments of the Moho are a consequence of several cycles of strike‐slip displacements on transverse faults known to be active here.

1 Introduction
Sikkim is an Indian state bordering Nepal, Tibet, and Bhutan (Figure 1a). The Sikkim Himalaya lies at the junction of multiple modes of deformation (England & Houseman, 1986; England & Molnar, 1997; Yin, 2000; Yin & Harrison, 2000).

To the west, the central Himalaya deforms by arc‐normal crustal shortening (Avouac, 2003; Avouac & Tapponnier, 1993), while to the east, northeast India undergoes oblique convergence across the Eastern Himalaya and E‐W convergence across the Indo‐Burma subduction zone (Kumar et al., 2015, Li et al., 2008, 2014; Lei & Zhao, 2016; Mitra et al., 2005; Ni et al., 1989), resulting in widespread deformation south of the Himalaya.

The whole thickness of the Sikkim Himalayan crust is seismogenic, displaying two distinct regimes of tectonic deformation: (a) crustal shortening within the Himalayan wedge and (b) strike‐slip motion within the underthrust Indian crust (Paul et al., 2015). Available 1‐D shear wave velocity models from previous seismological studies in the Sikkim Himalaya have highlighted first‐order variation in crustal structure (Acton et al., 2011; Singh et al., 2010). However, detailed 3‐D imaging of the major subsurface discontinuities (viz., the Main Himalayan Thrust (MHT), the Moho, and the midcrustal discontinuity) and their relationship to the active deformation has not been attempted, motivating our broadband seismological imaging of the crust and upper mantle structure of the Sikkim Himalaya.

Additionally, the lower Main Central Thrust (MCT) and the higher Peling Thrust (PT) within the Sikkim Himalaya form an arcuate geometry on the surface (Bhattacharyya & Mitra, 2009) (Figure 1a). This contrasts with adjacent segments of the Himalaya where these thrusts run parallel to the Himalayan arc, the Main Boundary Thrust, and the Himalayan Frontal Thrust (Yin, 2006). Correlation of the structural variations observed at the surface with crustal structure at depth is a prerequisite for kinematic analysis of active deformation and has never been attempted for the Sikkim Himalaya.

jgrb52303-fig-0001
Figure 1
Open in figure viewer
PowerPoint
(a) Topographic map of Sikkim highlighting the important Himalayan structures: Main Frontal Thrust (MFT), Main Boundary Thrust (MBT), Main Central Thrust (MCT), Peling Thrust (PT), Rangit Thrust (RT), and South Tibetan Detachment (STD). The traces of these Himalayan structures are taken from Bhattacharyya and Mitra (2009). The locations of the broadband stations within our network in Sikkim are shown as cyan triangle. (b) Map of the globe centered on Sikkim Himalaya, with location of teleseismic events (red stars) used in this study.
The first comprehensive image of the underthrusting Indian Plate beneath the Sikkim‐Darjeeling Himalaya was provided by Acton et al. (2011) using receiver function analysis. These results were from an approximately N‐S profile averaging a broad region across the Indian foreland basin (western Bengal Basin) and the Sikkim‐Darjeeling Himalaya. That study highlighted that the Moho dips gently to the north with local southward dip beneath Gangtok in the Lesser Himalaya. The MHT was seen to be dipping gently beneath the Lesser Himalaya, but its geometry farther north was obscured due to lack of high signal‐to‐noise data. Singh et al. (2010) used receiver function analysis to highlight the north dipping Moho beneath Sikkim with the presence of a “Moho doublet” at ∼40 km depth beneath the Lesser Himalaya. This was interpreted as eclogitization of the granulitic Indian lower crust, but the authors did not discuss the pressure‐temperature regime necessary to cause eclogitization at such shallow depth. Their study also explored the presence of a strong layer of anisotropy within a low‐velocity layer at 20–30 km depth. The starting models for inversion of receiver functions in both these studies (Acton et al., 2011; Singh et al., 2010) were based on the 1‐D density models proposed from an earlier study of gravity anomalies across the Sikkim Himalaya (Tiwari et al., 2006). Magnetotelluric studies by Patro and Harinarayana (2009) in Sikkim reported the presence of a conductive feature at a depth of 3–15 km. This was interpreted as molasse sediment from the Siwaliks and Lesser Himalaya or as trapped metamorphic fluids lubricating the underthrusting of the Indian Plate. Paul et al. (2015) studied the source mechanisms of the 2011 Sikkim earthquake and its aftershocks, which originated in the underthrust Indian crust, demonstrating the presence of active transverse strike‐slip faults beneath the Sikkim Himalaya. The 2006 Phodong earthquake, which originated within the Himalayan wedge, had a thrust fault mechanism highlighting the different deformation regimes in the underthrust Indian crust and the overriding Himalayan wedge.

These studies have indicated that the structure of the underthrust Indian crust beneath the Sikkim Himalaya plays an important role in partitioning along‐strike convergence across the Eastern Himalaya. Additionally, the configuration of the Himalayan thrusts at depth and the geometry of the detachment surface (MHT) play a significant role in strain accumulation within the Himalayan wedge, controlling the rupture size and geometry of megathrust earthquakes. Through a number of studies, we have developed a fairly consistent image of the large‐scale long wavelength variation of the crustal structure beneath the Eastern Himalaya (Mitra et al., 2005), the Sikkim Himalaya (Acton et al., 2011), the Nepal Himalaya (Nábělek et al., 2009; Schulte‐Pelkum et al., 2005), the Garhwal Himalaya (Caldwell et al., 2013), and the NW Himalaya (Rai et al., 2006). However, detailed subsurface architecture is still uncertain. The relationships between geological features observed on the surface and structures at depth are poorly understood. The detailed geometry of the MHT, the presence/absence of ramp‐flat‐ramp geometry, and the role of the Lesser Himalayan duplex in accommodating active deformation beneath the Sikkim Himalaya are yet to be established. In this study, we use receiver function analysis on seismological data acquired from a focused experiment of seven broadband stations spanning the Lesser, Higher, and Tethyan Himalaya. Our study provides a comprehensive shear wave velocity structure of the Sikkim Himalaya and 3‐D geometry of the MHT and the Moho. Finally, we examine the relationships between (i) the mapped geological features and the 3‐D crustal structure and (ii) the 3‐D crustal structure and the active faults within the underthrust Indian crust.

2 Data and Methodology
The seismological field experiment in the Sikkim‐Darjeeling Himalaya was done in two phases the first in 2005 and the second in 2008–2013. The first phase of the experiment was operated and funded through a joint project between University of Cambridge and Indian Institute of Technology (IIT) Kharagpur. The second phase was initiated from IIT Kharagpur with funding from Department of Science and Technology (DST), India, and then jointly operated through the UK‐India Education and Research Initiative (UK‐IERI) thematic partnership between IISER Kolkata and the University of Cambridge. Stations Gangtok (GTOK), Chungthang (CHTG), and Lachung (LCHG) were common in both phases. The other stations Namchi (NAMC), Rabangla (RABN), Mangan (MANG), and Yumthang (YUMT) were installed in 2008. The stations were deployed along an approximate N‐S profile across Sikkim (Figure 1a), extending from the Lesser Himalaya to the Tethyan Himalaya. NAMC and RABN were located in the Lesser Himalaya; GTOK, MANG, CHTG, and LCHG in the Higher Himalaya; and YUMT in the Tethyan Himalaya. GTOK was equipped with a Guralp CMG‐3TD seismometer with a flat velocity response between 120 s and 50 Hz. All the other stations had Guralp CMG‐3ESPCD instruments, with flat velocity response between 60 s and 100 Hz. All stations were equipped with CMG‐DCM/EAM data loggers that recorded data continuously at 100 samples per second. The data were time stamped using GPS synchronization.

2.1 Receiver Function Analysis
Receiver functions are the response of the near receiver structure to incoming teleseismic body waves and are made up of conversions and reverberations from discontinuities beneath the receiver site. A total of 1,430 teleseismic earthquakes (mb ≥ 5.5) from an epicentral distance range of 30° to 95° was recorded by the seven broadband stations (Figure 1b). Waveforms from these events have been used to compute P wave receiver functions. First, the horizontal components (north‐south and east‐west) were rotated into radial and tangential directions to isolate the P‐SV energy. This was followed by deconvolution of the vertical component from the radial and tangential components to remove source effects and common path effects between the source and the discontinuity. The deconvolved waveforms are called the radial and the tangential receiver functions. For a 1‐D isotropic velocity structure, the radial receiver function contains all the P‐to‐S converted and reverberating energy, while the tangential receiver function has no theoretical energy. However, for the real Earth, the tangential component has energy and its amplitude is used to assess the degree of deviation from the 1‐D isotropic assumption. We use the iterative time domain deconvolution technique of Ligorria and Ammon (1999) to compute the radial and tangential receiver functions. In this technique, the misfit between the radial component and the convolution of the vertical component with an iteratively updated spike train is minimized in the least squares sense. Iterations are continued up to a fixed number (i.e., 200) or until the misfit value falls below a threshold (set at 0.005). To eliminate high‐frequency noise, a low‐pass Gaussian filter of width 2.5 (corner frequency ∼1.2 Hz) is applied to the waveform. The receiver functions obtained through this time domain iterative technique are assessed for quality by the percentage fit to the observed radial waveform. For our analysis we selected only those waveforms which had a fit of ≥80%. Using this criterion, a total of 1,458 receiver functions was shortlisted for our study.

In order to enhance signal‐to‐noise ratio and increase coherence in the signal, receiver functions were stacked in the following ways: spatial stack, common conversion point (CCP) stack (Figure 2), and depth (H) verus VP/VS (K) stack. Spatial stacking is performed by averaging receiver functions in spatial bins using their piercing points (Figure 2a) on a given discontinuity (Moho, in our case). This has the advantage of highlighting the coherent features in the structure, irrespective of the station at which the waveform is recorded. In spatial stacking, all receiver functions are projected onto a selected profile and binned by distance along the profile (Figure 2b). Piercing points have been calculated using the crustal velocity structure from Acton et al. (2011) across the Sikkim Himalaya. The crustal thickness beneath the Himalaya is larger than that in the global 1‐D velocity models, so using this velocity structure has the advantage of computing Moho conversion depths using crustal rather than upper mantle velocities. The spatial plot is equivalent to a time section with the y axis representing time offset of the receiver function from the Pp arrival. The spatial plot has the advantage of aligning coherent conversions to highlight discontinuities but does not represent the true geometry of the discontinuity.

jgrb52303-fig-0002
Figure 2
Open in figure viewer
PowerPoint
(a) Map showing the location of stations (colored triangles) and corresponding receiver function piercing points on the Moho (plotted as plus sign with the same color), computed from the average crustal velocity model obtained from the results of Acton et al. (2011). (b) Spatial stack of receiver functions binned by their Moho piercing points at every 1 km interval and plotted along the profile AA urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0001 (A‐88.25° E, 27.05°N, and A urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0002‐88.90°E, 28.0°N). The positive amplitudes are colored black, and the negative amplitudes are colored grey. The Ps times corresponding to the MHT, the midcrustal interface, and the Moho are marked by magenta, green, and yellow dashed lines, respectively. (c) The CCP stack along the profile AA urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0003. The amplitude of the phases are scaled relative to the amplitude of the direct Pp phase, colored red for positive and blue for negative amplitudes. Horizontal smoothing has been applied using a Gaussian filter of width 2 km. The MHT, midcrustal interface, and Moho are marked as in Figure 2b.
CCP stacking uses similar piercing point information to spatial stacking but converts the arrival to depth beneath the surface (i.e., depth section). Additionally, in the CCP stack the amplitude of the P‐to‐S converted phase is color coded to highlight the impedance contrast across the discontinuity (Figure 2c). For the CCP stack, we employed the technique of Zhu (2000) where the receiver functions are backtraced using ray theory through the velocity model to their piercing‐point location. The receiver function amplitude values at each point are corrected for incidence angle effect and projected onto the raypaths according to the velocity model. The volume along the profile is then divided into bins of a certain size, and all the amplitudes within each bin are averaged. The bin size of our model was 5 km wide, 1 km long, and 0.6 km high. For a maximum frequency of 1.2 Hz, the vertical resolution is estimated to be 1.6 km. Note that both these stacked images (spatial and CCP) are 2‐D profiles and suppress information on the lateral variation of the subsurface discontinuities. Lateral variations imaged through 3‐D mapping of the discontinuities will be discussed in section 2.2.

In H‐K stacking, time domain waveforms are transformed into depth domain to estimate the thickness (H) and average VP/VS (K) of the crustal layer. The arrival times of P‐to‐S converted and multiple reverberating phases in a radial receiver function are dependent on layer thickness (H) and average VP/VS, for a given VP (Zhu & Kanamori, 2000). H‐K stacking uses a grid search over a range of H and K values and calculates the sum s(H,K) of the amplitudes of the phases (conversion and reverberations) at each grid point. A contour map of s(H,K) is maximized when all the three phases are stacked coherently and approximate values of H and K are obtained. The effects of lateral variation in the subsurface structure can be highlighted by performing the H‐K stack on receiver functions clustered in narrow bins of back azimuth and distance. In our analysis, receiver functions from each station were divided into clusters based on a narrow range of back azimuth and ray parameter. From all the stations, a total of 39 clusters was formed with significant number of receiver functions in each of them. The H‐K stack for each cluster has been estimated separately for both the entire crust (Moho) and the upper crust (midcrustal discontinuity). Figure 3 shows the H‐K stack for the Moho and midcrustal layer for receiver functions recorded at RABN in the back azimuth range 127°–157°, along with the synthetic receiver functions generated by forward modeling of these two discontinuities. We follow the same method to compute H‐K stacks for all the clusters at every station. The H‐K stacks for all the stations are shown in Figures 1–9 in the supporting information S1. The results are summarized in Table 1.

jgrb52303-fig-0003
Figure 3
Open in figure viewer
PowerPoint
(a) H‐K stack contour plot (between H and VP/VS) for RABN (cluster 8, back azimuth range 127°–157°). The estimated H‐K for the midcrustal layer and the Moho are marked by a blue and a red cross wire, respectively. The uncertainty bounds are shown by shaded rectangles. The H and K values for the midcrust are 27.5 ± 1.84 and 1.70 ± 0.014 and that of the Moho are 43 ± 1.84 and 1.665 ± 0.014, respectively. Plot of forward modeled receiver function stack corresponding to the estimated H‐K (b) for the midcrustal layer and (c) for the Moho. The stack of all receiver functions in the cluster is shown in blue, and that of the calculated synthetics is in red. The converted phase (Ps) and the reverberating multiples (PpPs and PpSs) are labeled on the plots. The station name, Gaussian width, percentage fit, and ray parameter are listed on the left from top to bottom.
Table 1. Summary of Receiver Function Back Azimuth Clusters and the H‐K Stacking Results
Midcrust Moho
Cluster BAZ No. of Depth Depth
No. Station no. (deg) RFs (km) VP/VS (km) VP/VS

1. NAMC 1 30–45 9 37.5 ± 2.66 1.690 ± 0.030 48.8 ± 2.66 1.765 ± 0.030
   2 54–72 13 36.0 ± 1.47 1.720 ± 0.010 50.0 ± 1.47 1.690 ± 0.010
   3 80–95 7 36.2 ± 3.66 1.718 ± 0.031 – –
   4 105–157 26 32.5 ± 2.18 1.675 ± 0.015 52.0 ± 2.18 1.736 ± 0.015
   5 295–313 6 34.5 ± 4.18 1.750 ± 0.041 43.0 ± 4.18 1.785 ± 0.041
2. RABN 1 33–54 36 33.5 ± 2.03 1.700 ± 0.014 46.1 ± 2.03 1.705 ± 0.014
   2 55–59 17 27.0 ± 4.40 1.760 ± 0.031 49.0 ± 4.40 1.640 ± 0.031
   3 60–72 74 32.5 ± 1.32 1.690 ± 0.010 48.5 ± 1.32 1.660 ± 0.010
   4 74–91 19 30.5 ± 1.38 1.720 ± 0.016 44.0 ± 1.38 1.725 ± 0.016
   5 94–105 14 26.5 ± 2.16 1.720 ± 0.018 45.0 ± 2.16 1.680 ± 0.018
   6 106–116 75 27.5 ± 1.29 1.690 ± 0.006 45.5 ± 1.29 1.690 ± 0.006
   7 117–126 29 27.5 ± 1.69 1.695 ± 0.014 46.5 ± 1.69 1.690 ± 0.014
   8 127–157 32 27.5 ± 1.84 1.700 ± 0.014 43.0 ± 1.84 1.665 ± 0.014
   9 277–308 24 30.0 ± 2.86 1.660 ± 0.013 50.0 ± 2.86 1.700 ± 0.013
3. GTOK 1 5–47 35 29.0 ± 2.74 1.700 ± 0.016 50.0 ± 2.74 1.775 ± 0.016
   2 49–57 21 31.0 ± 4.41 1.700 ± 0.027 55.0 ± 4.41 1.720 ± 0.027
   3 59–74 84 30.0 ± 1.17 1.740 ± 0.009 56.5 ± 1.17 1.730 ± 0.009
   4 76–98 46 29.0 ± 2.83 1.740 ± 0.013 – –
   5 102–152 222 34.0 ± 1.14 1.775 ± 0.006 58.0 ± 1.14 1.710 ± 0.006
   6 153–158 86 38.0 ± 1.15 1.700 ± 0.008 49.5 ± 1.15 1.785 ± 0.008
   7 235–256 12 29.0 ± 6.52 1.690 ± 0.027 57.5 ± 6.52 1.735 ± 0.027
   8 282–305 22 27.0 ± 3.26 1.760 ± 0.024 61.0 ± 3.26 1.750 ± 0.024
4. MANG 1 51–83 7 46.0 ± 8.98 1.700 ± 0.062 61.0 ± 8.98 1.790 ± 0.062
   2 107–110 4 44.0 ± 9.86 1.730 ± 0.012 62.5 ± 9.86 1.770 ± 0.012
   3 120–149 5 31.5 ± 6.83 1.750 ± 0.040 53.0 ± 6.83 1.675 ± 0.040
   4 152–172 6 35.0 ± 6.81 1.690 ± 0.040 55.0 ± 6.81 1.680 ± 0.040
5. CHTG 1 41–96 44 43.0 ± 2.56 1.730 ± 0.011 58.5 ± 2.56 1.710 ± 0.011
   2 106–138 71 38.0 ± 1.69 1.710 ± 0.008 58.0 ± 1.69 1.715 ± 0.008
   3 147–158 33 33.0 ± 2.49 1.700 ± 0.011 55.0 ± 2.49 1.720 ± 0.011
   4 293–306 5 47.0 ± 1.73 1.720 ± 0.017 59.0 ± 1.73 1.710 ± 0.017
6. LCHG 1 29–50 13 44.0 ± 6.04 1.770 ± 0.029 57.0 ± 6.04 1.740 ± 0.029
   2 51–97 38 47.0 ± 4.36 1.700 ± 0.014 63.5 ± 4.36 1.720 ± 0.014
   3 106–129 45 44.5 ± 4.99 1.700 ± 0.017 59.0 ± 4.99 1.710 ± 0.017
   4 134–208 30 44.0 ± 2.57 1.710 ± 0.016 56.5 ± 2.57 1.690 ± 0.016
7. YUMT 1 27–42 18 47.0 ± 1.82 1.690 ± 0.020 58.0 ± 1.82 1.665 ± 0.020
   2 45–68 63 – – 53.0 ± 1.87 1.740 ± 0.018
   3 70–89 24 – – 59.0 ± 3.17 1.700 ± 0.030
   4 105–140 106 42.0 ± 1.75 1.700 ± 0.008 66.2 ± 1.75 1.740 ± 0.008
   5 147–158 37 33.0 ± 3.90 1.720 ± 0.012 60.0 ± 3.90 1.750 ± 0.012
   2.2 Joint Inversion for Shear Wave Velocity Structure and 3‐D Mapping of Discontinuities
   Receiver function stacks from every cluster beneath each station are jointly inverted with Rayleigh wave group velocity dispersion data to constrain the shear wave velocity structure of the crust and uppermost mantle. Receiver functions are sensitive to impedance‐contrast boundaries, while surface wave dispersion data are sensitive to vertical averages of shear wave velocity beneath the seismograph site. Joint inversion of the two data sets complements each other and provides optimal shear wave velocity structure. Rayleigh wave group velocity dispersion data, corresponding to the station locations in Sikkim, were extracted from regional surface wave tomography results of India and Eurasia (Gilligan, 2014). These dispersion curves provide group velocities at discrete periods between 5 and 70 s. For the joint inversion, we use the linearized least squares inversion algorithm of Herrmann and Ammon (2004). In this method, an a priori value controls the influence of each data set by trading off between the two. A forward model is estimated based on the values of H and VP/VS from the H‐K stacking results. This forward model is taken as the initial model for the inversion and parameterized by thin layers of fixed thickness and velocity. The final model, with a minimum number of interfaces, which fits both the data sets, is obtained through iterative least squares inversion. The a priori weighting between the receiver function and surface wave dispersion data is set to 0.8 and 0.2, respectively. The final model is then coarsely parameterized by combining layers with similar velocities to obtain a minimum layer model. Fit to the observed receiver function and dispersion data, for both the models (minimum interfaces and minimum layers) are compared to highlight the main features in the crust and uppermost mantle structure. Figure 4 summarizes the joint inversion results for RABN in the back azimuth range of 127°–157°. The main features of the crustal structure are the thin (2–4 km) low‐velocity layer (LVL) in the shallow crust and the two major positive impedance contrasts, in the midcrust and at the Moho. We perform uncertainty analysis on each of these features and obtain a depth uncertainty of ±2 km and velocity (VS) uncertainty of ±0.05 km/s. The joint inversion results for all the stations are depicted in Figures 10–21 in the supporting information S1.

jgrb52303-fig-0004
Figure 4
Open in figure viewer
PowerPoint
Joint inversion result of receiver functions and Rayleigh wave group velocity dispersion data for RABN (cluster 8, back azimuth range 127°–157°). (a) Plot of fit between the observed dispersion data (black circles with error bars) and the synthetic dispersion data computed from the minimum interface model (blue) and the minimum layer model (red). (b) Plot of fit between the observed receiver function stack (black dash) and synthetic receiver function stack computed from the models plotted in Figure 3c. (c) Plot of minimum layer model (blue) and minimum interface model (red) obtained by fitting the data. The starting mantle half‐space model is plotted in grey (dashed line). The inferred MHT, midcrust, and Moho are labeled on the plot.
To observe the lateral variation of the major discontinuities (the MHT and Moho) beneath the Sikkim Himalaya, we devised a method to obtain the map coordinates of a given discontinuity and its spatial depth variation. The depth of the discontinuities (the MHT and Moho) and the associated VS for a particular cluster is obtained by joint inversion of receiver functions and Rayleigh wave group velocity dispersion data. The piercing point for each receiver function is calculated for the inferred depth (of the discontinuity) using the obtained velocity model. The piercing point gives the spatial location of the discontinuity at a given depth. This procedure is followed for all receiver functions which provides a distribution of points in three dimensions, representing the depth to a given discontinuity. We fit a surface through these points using bicubic interpolation to obtain a lateral variation map of the subsurface discontinuity. The bicubic interpolation method fits a continuous surface on a unit square with continuous derivatives. By patching together such continuous bicubic surfaces with continuous derivatives across the boundaries, we obtain a smoothed discontinuity surface. This has the advantage of lateral correlation of the discontinuity across the region but can underestimate steep slopes or abrupt change in depth to the discontinuity. Using this method, we construct 3‐D maps of the MHT and the Moho beneath the Sikkim Himalaya.

3 Results
3.1 Two‐Dimensional Profiles: Spatial and CCP Stacking Results
Receiver functions from all stations were spatially stacked along the AA urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0004 profile in 1 km bins (Figures 2a and 2b). The profile is aligned with the station locations to maximize the region covered by the receiver functions. Positive amplitudes are colored black, while the negative amplitudes are grey. The Ps conversion from the MHT, midcrust, and Moho are marked by magenta, green, and yellow dashed lines, respectively. The shallow low‐velocity layer, with a negative arrival, is identified as the MHT. This appears at a time offset of ∼1 s below the southern end of the profile (NAMC) and with the offset gradually increasing northward to ∼3 s (YUMT) and indicates the northward dip of the structure. We observe three significant steps on the MHT at distances of ∼35 km, 80–90 km, and ∼120 km along the profile. These steps indicate a sharp change in northward dip on the MHT. The midcrustal Ps is at a time offset of ∼3.5 s for the first 40 km along the profile. This offset gradually increases to ∼5 s at 60 km along the profile. At this point, a sharp decrease in the arrival time of the midcrustal Ps is observed (from ∼4 s to ∼3 s), which possibly corresponds to a local southward dip of the midcrust. Farther north, the arrival time from the midcrust increases steadily northward from ∼3 s to ∼5 s. The Moho Ps phase shows similar characteristics to the midcrustal phase. At the southern end of the profile, the offset time of the Moho Ps phase is ∼6.5 s, increasing to ∼7.5 s at 45 km along the profile. This is followed by a sharp decrease in the offset time, indicating Moho imbrication or local southward dip. Beyond a distance of 60 km along the profile, the Moho Ps again increases gradually to ∼7 s. Several more arrivals are also observed in addition to the ones discussed above. Two distinct positive phases are observed earlier than the MHT arrival at distances of 80–135 km and 115–135 km along the profile. These mark discontinuities within the Himalayan wedge, possibly associated with thrust imbrication underneath the Higher Himalaya. Another positive arrival is observed immediately following the MHT arrival. This is prominently visible at distances of 75–135 km along the profile and becomes less distinguishable elsewhere. This phase appears to track the MHT and deepens northward. This could be the uppermost crustal layer of the underthrust Indian Plate.

The CCP stack has been constructed along the same profile (AA urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0005, Figure 2a) and provides a depth section across the Sikkim Himalaya (Figure 2c). Impedance contrast discontinuities with positive gradient are colored red, and those with negative gradient are colored blue. The intensity of the color is scaled by the ratio of the phase amplitude to the direct arrival Pp. The MHT corresponds to the negative impedance contrast arrivals seen in the shallower part of the crust (Caldwell et al., 2013), while the midcrust and Moho are positive impedance contrast arrivals. The MHT, the midcrustal interface, and the Moho are marked by the same colors as for the spatial plot discussed above. To first order, the MHT, midcrust, and Moho are all observed to dip to the north. The MHT has two significant changes in dip, one beneath GTOK and the other beyond LCHG. We ascribe these to the presence of ramps on the MHT connected by flat sections. The Moho displays second‐order dip variations at a number of places, the strongest among these is the region underneath RABN. Here we observe an apparent Moho doublet, possibly due to projection of a three‐dimensional Moho onto a 2‐D profile. This feature will be discussed further in section 3.3.1. The Moho is also observed to dip locally southward beneath GTOK and CHTG. This could be an effect of the flexure of the seismogenic crust resulting in imbrication of the Moho, which has been observed beneath Nepal Himalaya (Hirn et al., 1984). The midcrustal boundary displays a similar geometry to the Moho. Southward dip and imbrication of this boundary are observed beneath GTOK and CHTG. The lower crustal layer, between the midcrustal discontinuity and the Moho, appears to have similar thickness across the Sikkim Himalaya. In addition to these first‐order near‐horizontal crustal discontinuities, a number of steeply dipping (∼65–70°) low‐velocity structures are observed on the CCP at distances between 55 km and 75 km along the profile (beneath MANG and CHTG). These structures are marked by dashed lines within an ellipse (Figure 2c) and are observed to intersect the Moho and the midcrustal discontinuity. These low‐velocity zones may be active transverse structures within the underthrust Indian crust, similar to the ones which caused dextral strike‐slip earthquakes beneath the Sikkim Himalaya (Paul et al., 2015). A couple of strong negative arrivals are observed in the CCP, between stations NAMC and RABN at a depth of ∼20 km and between stations RABN and GTOK at depth range 30–40 km. Through forward modeling of the RFs, we have ascertained that these are multiples from the MHT negative arrival.

3.2 H‐K Stacking Results
The Lesser Himalayan crust is sampled by NAMC and RABN. H‐K stacks show the presence of lateral variation in the depth to the Moho and to the midcrustal discontinuity beneath both of these stations. The Moho depth beneath NAMC and RABN varies from 43 km to 52 km, with deeper segments at the N‐NW and SE back azimuths and the shallowest segment in‐between (Figure 5a and Table 1). The midcrustal depth beneath the Lesser Himalaya varies between 27 km and 37 km, with E‐W lateral variation. The shallowest segment lies in the middle with deeper segments to the east and to the west (Figure 5b). The VP/VS ratio beneath the Lesser Himalaya varies between 1.67 and 1.77 and increases from the east to the west. The mean values of VP/VS for the upper crust and the whole crust are ∼1.70 and ∼1.72, respectively.

jgrb52303-fig-0005
Figure 5
Open in figure viewer
PowerPoint
Contour plot of depth to (a) the Moho and (b) the midcrustal layer and associated VP/VS variation for (c) the whole crust and (d) the crustal layer above the midcrustal discontinuity, beneath the Sikkim Himalaya. The depth and VP/VS for each cluster at a given station is projected on the map (r,θ) using the central back azimuth (θ), chosen from the back azimuth range of the cluster, and a fixed distance (r, proportional to its depth) from the station. The contoured surface is drawn by triangulation, and the variation in depth and VP/VS is color coded. The grey triangles represent the stations, and the crosses represent a group of RF piercing points where actual measurements were made.
Beneath GTOK in the Higher Himalaya, the Moho depth varies between 50 km and 58 km (west to east) and has a gentle southward dip along the SE back azimuth (Figure 5a). The midcrustal layer has a shallow segment at ∼28 km in the north and deepens to ∼36 km to the south and the east (Figure 5b). Significantly low crustal VP/VS is observed just west of GTOK (Figures 5c and 5d). Farther north within the Higher Himalaya, MANG, CHTG, and LCHG shows a gradual northward increase in crustal thickness without any significant lateral heterogeneity. For MANG, the depth to the midcrustal discontinuity and the Moho increases northward from 35 km to 46 km and 53 km to 62 km, respectively. The average VP/VS for the upper crust and the whole crust beneath both GTOK and MANG are found to be ∼1.71 and ∼1.73, respectively. The Moho depth beneath CHTG increases northward from 55 km to 59 km but has a southward dip to the south of the station. The midcrustal depth also increases northward from 33 to 47 km. The Moho depth beneath LCHG varies from 57 km to 61 km, increasing to the north and the east. The depth of the midcrustal layer is observed to vary from 44 km to 47 km (Figures 5a and 5b). The average VP/VS for both the upper crust and whole crust beneath both CHTG and LCHG is ∼1.71 (Figures 5c and 5d).

The Tethyan Himalaya, sampled at YUMT, shows a Moho depth variation from 58 km to 60 km, with a shallow isolated segment of 53 km in the NE back azimuth (Figure 5a). The midcrustal layer uniformly dips to the north from 42 km to 47 km. The VP/VS for the upper crust varies between 1.69 and 1.72, with an average value of ∼1.70. The average VP/VS for the whole crust is ∼1.73. This reveals that the average VP/VS for the Indian upper crust is slightly lower than that of the whole crust (Figures 5c and 5d) indicating that the underthrust lower Indian crust is more mafic in composition.

3.3 Joint Inversion Results
Joint inversion of receiver functions and Rayleigh wave group velocity dispersion data has been used to constrain the shear wave velocity structure beneath the Sikkim Himalaya. The starting model for the joint inversion is built from the H‐K result. The joint inverted shear wave velocity model for RABN in the back azimuth range of 127° to 157° is plotted in Figure 4 as an example. We discuss the joint inversion results region wise for the Sikkim Himalaya and provide a station‐wise summary in Table 2. We have overlaid the shear wave velocity models, obtained by joint inversion, onto the CCP stack (Figures 6a and 6b) along the profile AA urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0006 to compare and contrast the results. The major crustal discontinuities, splay faults, and the inferred transverse structures beneath the Lesser, Higher, and Tethyan Himalaya with the average VS listed for each layer are highlighted in Figure 6c. A comparison of the Moho depths obtained from H‐K stacking and joint inversion results reveals a good agreement (Figure 6d), except for the southern back azimuth in RABN and northern back azimuth in MANG. The differences could be due to deviation from the assumed VP of 6.4 km/s in the H‐K analysis. Such deviations could explain the anomalous VP/VS values in these regions (Figure 5c).

jgrb52303-fig-0006
Figure 6
Open in figure viewer
PowerPoint
(a) The profile AA urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0007 shown as brown dashed line in the map along with the source mechanisms from (Paul et al., 2015) in this region. The mechanisms at depths ≤20 km are colored grey, while those of deeper events are colored black. The earthquakes deeper than 20 km have a dominant strike‐slip component. The stations are represented by yellow triangles. (b) The CCP stack of receiver functions (Gaussian width 2.5) along the profile AA urn:x-wiley:jgrb:media:jgrb52303:jgrb52303-math-0008 overlain with inverted models (grey) for each cluster. The relative amplitude of the phases with respect to direct arrival is scaled. Positive amplitudes are colored red, and negative are in blue. Important structural features like the PT, MCT, MHT, and midcrustal discontinuity are highlighted by dashed yellow lines. Oblique black lines identify the transverse structures seen in the CCP. (c) A schematic diagram based on the inverted models, and the CCP stack is shown for the region. The MHT and other thrust sheets are represented by blue, the midcrust in brown, and the Moho in black dashed lines. The active fault features (TS) are shown as cyan line segments. The average VS in each of the region is also specified. (d) Comparative Moho depths from H‐K stacking results (green rectangles) and joint inversion results (blue triangles) with error bars. Data points from each of the stations are arranged from the south to the north (based on the back azimuth range of the cluster).
Table 2. Summary of the Joint Inversion Results
Himalayan Indian Indian Indian Upper
LVL (MHT) wedge upper crust lower crust whole crust mantle
Depth VS VS Thickness VS Thickness VS Thickness VS VS
BAZ of layer of layer of layer of layer of layer of layer of layer of layer of layer Sn
Station No. (deg) (km) (km/s) (km/s) (km) (km/s) (km) (km/s) (km/s) (km) (km/s)
NAMC 1 30–45 10.5 3.21 3.28 33 3.54 19 3.83 52 3.63 4.23
2 54–72 8 3.15 3.31 33 3.48 12 3.88 45 3.58 4.07
3 80–95 6a 3.16 3.29 27 3.28 24 3.77 51 3.58 4.26
4 105–157 6a 3.13 3.30 27 3.38 24 3.79 51 3.60 4.22
5 295–313 7.5 3.14 3.34 33 3.55 11 3.73 44 3.59 4.19
RABN 1 33–54 7a 3.16 3.26 28 3.41 17 3.90 45 3.62 4.19
2 55–59 6a 3.07 3.37 26 3.35 18 3.88 44 3.58 4.14
3 60–72 7a 3.16 3.26 28 3.41 17 3.90 45 3.62 4.19
4 74–91 6a 3.25 3.31 28 3.42 16 3.88 44 3.60 4.02
5 94–105 10 3.26 3.29 24 3.33 20 3.84 44 3.63 4.33
6 106–116 9.5 3.10 3.22 24 3.39 28 3.78 52 3.65 4.20
7 117–126 9.5 3.06 3.25 24 3.44 29 3.83 53 3.69 4.26
8 127–157 9.5 3.10 3.25 24 3.48 27 3.84 51 3.69 4.07
9 277–308 10.5 3.04 3.31 25 3.38 27 3.83 52 3.69 4.26
GTOK 1 5–47 10 3.15 3.24 25 3.32 27 3.76 52 3.60 4.30
2 49–57 10.5 3.19 3.24 28 3.39 26 3.86 54 3.66 4.36
3 59–74 6a 3.29 3.33 28 3.36 26 3.80 54 3.60 4.24
4 76–98 11 3.26 3.30 21 3.25 24 3.66 45 3.57 4.07
5 102–152 12 3.26 3.28 35 3.66 20 3.79 55 3.66 4.23
6 153–158 12 3.28 3.27 36 3.67 18 3.73 54 3.63 4.26
7 235–256 7 3.29 3.30 40 3.54 14 3.85 54 3.63 4.24
8 282–305 8a 3.24 3.28 27 3.35 27 3.85 54 3.63 4.39
MANG 1 51–83 13 3.18 3.32 43 3.63 11 3.93 54 3.67 4.19
2 107–110 13 3.25 3.25 36 3.56 17 3.71 53 3.62 4.21
3 120–149 9 3.25 3.39 29 3.48 25 3.83 54 3.63 4.30
4 152–172 10 3.19 3.25 29 3.44 26 3.79 55 3.64 4.20
CHTG 1 41–96 11a 3.22 3.25 40 3.53 16 3.76 56 3.76 4.24
2 106–138 12.5 3.29 3.25 37 3.59 17 3.67 54 3.57 4.23
3 147–158 15 3.28 3.31 30 3.46 22 3.74 52 3.60 4.22
4 293–306 15 3.13 3.26 36 3.59 19 3.70 55 3.63 4.24
LCHG 1 29–50 16 3.22 3.26 41 3.64 14 3.69 55 3.59 4.21
2 51–97 16 3.33 3.26 42 3.67 16 3.64 58 3.60 4.28
3 106–129 17 3.35 3.26 37 3.57 24 3.72 61 3.65 4.28
4 134–208 16 3.22 3.27 40 3.63 21 3.72 61 3.66 4.24
YUMT 1 27–42 25 3.36 3.34 47 3.56 12 3.96 59 3.72 4.28
2 45–68 25 3.36 3.32 – – – 3.62 54 3.64 4.21
3 70–89 25 3.34 3.35 – – – 3.69 57 3.65 4.17
4 105–140 19 3.36 3.31 37 3.47 24 3.81 61 3.67 4.28
5 147–158 19.5 3.14 3.35 35 3.87 24 3.74 59 3.68 4.37
a The MHT depths are thick LVL (4–6 km) with the given depth as upper bound of the LVL. These may be a combination of the MHT and its imbricate faults above. The uncertainty in depth is ±2 km and in VS is ±0.05 km/s.
3.3.1 Lesser Himalaya
NAMC and RABN are situated on the low‐grade metamorphic rocks of the Lesser Himalaya. Joint inversion results highlight the presence of lateral heterogeneity beneath both of these stations (Table 2 and Figure 6). The MHT is demarcated by a LVL at shallow depth. South of NAMC, it is observed at a depth of ∼8 km, increasing to ∼10 km northward, between NAMC and RABN. Farther to the north, beyond RABN, the LVL’s depth reduces to ∼7 km (Table 2). The deeper segment of the MHT is also observed to the east of both NAMC and RABN and attests to the 3‐D configuration of this boundary. This will be discussed in detail later (section 3.4.1 and Figure 7). In the 2‐D representation (Figure 6), this lateral heterogeneity is masked because of averaging effects, and the MHT appears as a flat beneath the Lesser Himalaya (depth ∼8 km). It is followed by a ramp (localized dip ∼10∘) south of GTOK (10–12 km). In several places across the Lesser Himalaya, the MHT appears as a thick (4–6 km) LVL, possibly representing a combination of the MHT and shallower imbricate faults. Beneath NAMC and RABN, the average VS of the LVL is modeled to be ∼3.15 km/s and that of the Himalayan wedge (above the MHT) to be ∼3.3 km/s. The Moho and the midcrustal layer also reveal large lateral variation in depth across the region. Shallower segments of the Moho (∼45 km) are observed to the west of both NAMC and RABN. To their east, the Moho deepens to reach a maximum depth of ∼52 km and then again shallows to ∼45 km. These structures dip approximately E‐W and appear as ridges in 3‐D. These structures could be due to imbrication of the crust (discussed in detail in section 3.4.2) and are clearly observed in the 3‐D plot of the Moho (Figure 8) but appear as a Moho doublet in 2‐D representation (Figure 6). The midcrustal layer has deeper section (∼33 km) to the west of both NAMC and RABN, shallows to ∼25 km eastward, and again deepens to ∼28 km farther east. A similar observation was also made from the H‐K stacking results with comparable depth values (Figure 5b). However, this lateral variation is not apparent in the 2‐D representation (Figure 6) due to averaging of receiver function amplitudes. The average VS for the upper crust and the lower crust beneath the Lesser Himalaya is modeled to be ∼3.42 km/s and ∼3.82 km/s, respectively, indicating that the lower crust is more mafic in composition than the upper crust. The average VS for the whole crust is ∼3.63 km/s. The VS for the uppermost mantle beneath the Lesser Himalaya is ∼4.22 km/s.

jgrb52303-fig-0007
Figure 7
Open in figure viewer
PowerPoint
Three‐dimensional plot of the MHT surface: (a) map view, (b) schematic illustrating the dome structure observed in map view, (c) view from the E‐SE direction, and (d) view from the NE direction. The MHT topography (depth 8–25 km) is color coded. The receiver function piercing points are plotted as black asterisks, and the stations are represented by white inverted triangles. The outcrop of the PT and MCT are plotted on top. In map view, depth isolines are plotted as white (8–9 km) and blue (10–12 km) dashed lines. These isosurfaces are joined by cyan dashed lines, representing oblique ramps. The piercing points from NAMC, RABN, GTOK, and MANG are denoted as N, R, G, and M, respectively, in the schematic plot (Figure 7b). In Figure 7d, the dashed black lines join the MHT 3‐D surface to the outcrop. The thick magenta line represents the surface trace of the MHT locking line taken from Ader et al. (2012). A movie S1 provided in the supporting information provide a perspective on the MHT dome structure.
jgrb52303-fig-0008
Figure 8
Open in figure viewer
PowerPoint
Map view of the Moho (depth 44–61 km) topography. The receiver function piercing points are plotted as black asterisks, and the stations are plotted as white triangles. The outcrops of PT and MCT are plotted as black lines. Earthquake source mechanisms (depth ≥20 km) from Paul et al. (2015) are overlay plotted.
3.3.2 Higher Himalaya
Receiver functions from GTOK, MANG, CHTG, and LCHG sample the crystalline complex and high‐grade metamorphic rocks of the Higher Himalaya. The lateral variation in structure observed beneath the Lesser Himalaya continues farther north. Beneath GTOK, in the NW back azimuth, the MHT is at a depth of ∼7 km. This is surrounded by deeper segments (10–12 km) eastward and southward, resulting in an east dipping MHT west of the station (Figure 7). This feature was not observed in the 2‐D image due to averaging effects (Figure 6). North of GTOK, the structural variation is mainly north‐south. The MHT depth beneath MANG varies from ∼10 km in the south to ∼13 km in the north, with a dip of ∼8∘. Beneath CHTG, the MHT exhibits a southward dip as it shallows from ∼15 km in the south to ∼13 km in the north. The MHT beneath LCHG is at a depth of ∼16 km. The average VS of the LVL beneath GTOK, MANG, and CHTG is ∼3.23 km/s and increases marginally beneath LCHG to ∼3.28 km/s. The average VS of the Himalayan wedge is modeled to be ∼3.29 km/s. From south to north, the average VS of the LVL progressively approaches that of the Himalayan wedge.

The lateral variation in the Moho depth beneath GTOK is highlighted by the presence of a shallow Moho (∼45 km) beneath east of GTOK, while in all other directions the depth is ∼54 km. Comparing with Moho depth beneath RABN, we observe a locally elevated segment of the Moho surrounded by deeper segments. This appears as an imbrication in the 2‐D profile (Figure 6), while its 3‐D shape is an elongated dome (Figure 8). Acton et al. (2011) reported a southward dipping Moho based on a 2‐D study, consistent with our observed geometry. Beyond GTOK, however, the Moho dips northward with minor lateral variations. Beneath MANG, the Moho is at a depth of ∼54 km. Beneath CHTG it varies from 52–56 km, progressively dipping northward. Beneath LCHG, we observe significant lateral variations with a deeper Moho (∼60 km) in the south and the east, while shallower segments (∼56 km) are observed to the north and the west. As a result, we observe southward and eastward dipping segments of the Moho beneath LCHG (similar to Figure 5a). In 2‐D profile (Figure 6), the eastward dip is masked due to averaging, but the southward dip is observable and could be the result of imbrication of the lowermost crust. The average Moho depths beneath GTOK, CHTG, and LCHG obtained in this study matches with the results of Acton et al. (2011). In addition, our study highlights the lateral variation in the crustal structure.

The midcrustal layer is also observed to vary laterally beneath the Higher Himalaya. Beneath GTOK, it is at a depth of ∼27 km) in the northern back azimuth and deepens to ∼36 km to the south, indicating a southward dip (Figures 6 and 5b). For MANG, the midcrustal layer dips gently northward from a depth of ∼29 km to ∼43 km. Farther north, beneath CHTG, the midcrustal layer shallows to ∼30 km in the southern back azimuth and then continues to dip northward reaching a depth of ∼37 km. This results in a local increase of the northward dipping angle to ∼16∘ from ∼10∘. Beneath LCHG, a shallow segment (∼37 km) is seen to the east of the station. In all other directions, the midcrustal layer is at a depth of ∼41 km. The average VS of the upper crust increases gradually from ∼3.45 km/s to ∼3.63 km/s, while the average VS of the lower crust reduces from ∼3.8 km/s to ∼3.7 km/s northward. This increase in VS of the upper crust northward indicates mafic composition. The reduction in velocity of the lower crust could be influenced by the presence of oblique transverse structures beneath the Higher Himalaya, as observed in the CCP stack (Figures 2c and 6). The average VS of the entire crust is modeled to be ∼3.63 km/s, and that of the uppermost mantle is ∼4.22 km/s, similar to the Lesser Himalaya.

3.3.3 Tethyan Himalaya
Although YUMT is located in the Higher Himalaya, the receiver function raypaths converging at the station mostly sample the crust beneath the Tethyan Himalaya. Our joint inversion results indicate that the MHT dips steeply beneath this region. Its depth increases from ∼19 km in the south to ∼25 km in the north with a dip of ∼16∘. The average VS of the MHT LVL is modeled to be ∼3.31 km/s. This is slightly higher than that in the Lesser and Higher Himalaya but is nearly equal to the VS in the Himalayan wedge (∼3.33 km/s). This gradual increase in the LVL VS from the Lesser Himalaya to the Tethyan Himalaya is probably a result of the transition from frictionally locked to creeping behavior of the MHT decollement. An additional low‐velocity layer is also observed just above the MHT. This corresponds to the MCT, which splays from the MHT farther to the north. The Moho is at a depth of ∼59 km beneath YUMT, with a marginally elevated segment (∼56 km) in the NE back azimuth (Figure 8). The midcrustal layer could not be identified by joint‐inversion modeling in two clusters of YUMT. This may be due to destructive interference of the midcrustal phase with multiples from shallow layers in the Himalayan wedge. This hypothesis has also been confirmed by forward modeling. In the remaining clusters, the depth to the midcrustal layer drastically increases from ∼35 km to ∼47 km northward, resulting in a tapered lower crust, also observed in previous studies (Mitra et al., 2005). The average VS of the lower crust beneath the Tethyan Himalaya is ∼3.76 km/s, which is higher than the Higher Himalaya. However, the upper crust beneath both regions has similar average VS (∼3.63 km/s). As a result, the average VS of the entire crust beneath the Tethyan Himalaya increases slightly to ∼3.67 km/s. The average VS of the uppermost mantle is modeled to be ∼4.26 km/s, similar to the Lesser and Higher Himalaya.

To first order, the MHT, midcrustal interface, and Moho dip to the north at angles of ∼9∘  ∼10∘, and ∼7∘, respectively. However, there are observable second‐order variations in the depth of each of these discontinuities. The MHT shows a ramp‐flat‐ramp geometry with a gentle northward dip beneath the Lesser Himalaya and a steep dip beneath the Tethyan Himalaya. Imbricate faults (MCT and PT) splay off the MHT beneath the Higher Himalaya. The Moho has several secondary undulations with significant southward dips beneath the Lesser and the Higher Himalaya and lateral heterogeneity beneath the Lesser Himalaya. The midcrustal layer also displays southward dips and lateral variations similar to the Moho. The thickness of the Indian crust (between MHT and the Moho) varies between ∼35 km and ∼42 km, which is similar to the thickness variation observed in the Indian Shield crust. Beneath the Tethyan Himalaya the underthrust Indian lower crust is seen to be marginally tapered. A number of oblique low‐velocity layers, within the underthrust Indian crust, are observed beneath the Higher Himalaya (Figure 6). These layers are near perpendicular to the profile and therefore are oriented NW‐SE. They dip at an high angle to the first‐order crustal discontinuities and extend from the MHT to the Moho, intersecting the entire underthrust Indian crust. These structures are discussed in detail later.

3.4 Three‐Dimensional Mapping of Subsurface Structures
The results of the CCP stack, H‐K stack, and joint inversion highlight the presence of significant lateral variation in the geometry of the MHT and the Moho beneath the Sikkim Himalaya. We use the shear wave velocity model obtained from joint inversion to map the depths of these discontinuities. This allows us to image the 3‐D variation in the subsurface structures.

3.4.1 Geometry of The Main Himalayan Thrust
Following the procedure outlined in section 2.2, we map the 3‐D configuration of the MHT. Our results are plotted in Figure 7, viewed from different directions, with the 3‐D MHT surface being color coded by depth. The piercing points of receiver functions are plotted as black asterisks, and stations are plotted as white triangles. The piercing points from four stations NAMC, RABN, GTOK, and MANG constrain the surface beneath the Lesser Himalaya (Figure 7a). Each of these stations has four clusters of piercing points. On closer inspection it is evident that each of the stations has at least two sets of piercing points at different depths which indicates that the receiver functions sample the edges or slopes of the 3‐D surface of the discontinuity. To highlight the structure defined by the surface, we draw dashed isolines of depth on the map view (Figure 7a) and plot a schematic (Figure 7b) based on piercing points. The shallow (8–9 km) isolines are drawn in white and the deeper (10–12 km) ones in blue. These are connected by cyan lines. We observe two oblique ramps (Figures 7a and 7b), one dipping to the NE and the other dipping S‐SE. However, we cannot rule out the possibility of these oblique ramps being a combination of number of ramps with different orientations. The same is true for the flat‐top portion which could be rounded or of any irregular shape. Each of these combinations, however, would result in a dome shape of the MHT beneath the Lesser Himalaya. To investigate the 3‐D structure of the MHT, we view the block from two different angles. Viewing the block from the E‐SE direction (Figure 7c) highlights the ramp‐flat‐ramp geometry of the MHT, with the shallower ramp beneath the Lesser Himalaya and the deeper ramp underneath the Tethyan Himalaya. The two ramps are connected by a flat (dip ∼5∘). The ramp beneath the Lesser Himalaya is smaller and has a gentler dip of ∼7∘, while the one beneath the Tethyan Himalaya is larger and has a steeper dip of ∼15∘. Viewing the block from the NE (Figure 7d) shows that the ramp beneath the Lesser Himalaya is domed in shape. This perspective also highlights the steep dip of the ramp beneath the Tethyan Himalaya. The arcuate shape of the PT and MCT on the surface (Figure 7d) matches the spatial extent of this dome structure on the MHT in the subsurface. We conjecture that the arcuate shape of the PT and the MCT (observed on regional outcrop map) is the surface expression of this subsurface dome‐shaped geometry of the MHT. The PT and the MCT splay off the MHT close to where the two ramps have been observed (Figure 7d). From this geometry, we infer that these splays will also be arcuate in shape in the subsurface. Our inference is supported by the observed dips of the PT and the MCT measured on outcrops, which reveal that the structure is a doubly plunging anticline (dome shape) (Bhattacharyya & Mitra, 2009). Moreover, Ray (2000) demonstrated that the observed ∼60 km N‐S spatial deflection of the arcuate shape of the PT and MCT cannot be produced by crosscutting of topography and planar thrust sheets, which is consistent with our results.

3.4.2 Geometry of the Moho
The 3‐D geometry of the Moho (Figure 8) is obtained in a similar way to that of the MHT. The precision and reliability of the 3‐D surface constructed from the piercing points are tested in the same way. The CCP stack results (Figure 6) suggest that the Moho dips to the north from the Lesser Himalaya. However, the 3‐D surface map shows that the significant dip of the Moho initiates beneath the Higher Himalaya and continues beyond the Tethyan Himalaya. Beneath the Lesser Himalaya and the Higher Himalaya, we observe a significant dome structure on the Moho. This dome structure is slightly staggered from the dome in the MHT but within the arcuate shape of the PT and the MCT. The crest of the Moho dome lies below the stations GTOK and MANG. Similar but smaller domes are also observed in southeastern (88.9°E, 27.3°N) and southwestern (88.2°E, 27.3°N) edges of the map. The CCP stack along an oblique profile overlapped these dome shapes in the Lesser and the Higher Himalaya to form an apparent double Moho (Figure 6). In the NE corner of the map, we observe that the Moho shallows to a depth of 55–56 km. This shallow portion is surrounded by deeper segments of the Moho. This could be the remnant signature of a dome which is now steeply dipping beneath the Tethyan Himalaya. On a larger scale, these domes are intersected by linear, deeper segments of the Moho trending NW‐SE. The significance of these alternating shallow and deep segments of the Moho is discussed along with the transverse structures in the lower crust in section 4.2.

4 Discussion
4.1 Crustal Architecture of the MHT and Its Relationship to the Surface Structures
We present a detailed image of the Himalayan wedge, the underthrusting Indian crust and the detachment surface (MHT) along which the Indian Plate underthrusts the Sikkim Himalaya. The top of the underthrusting plate is highlighted by a LVL which marks the Main Himalayan Thrust (Acton et al., 2011; Nábělek et al., 2009; Schulte‐Pelkum et al., 2005). This represents a fault zone which facilitates the relative motion between the Indian Plate and the overriding Himalayan wedge. It is observed that the Himalayan wedge increases in thickness northward and has an average VS of ∼3.33 km/s. From our models, we observe that the MHT LVL has a thickness of ∼2 km and an associated velocity of 3.1–3.2 km/s for stations south of the MCT zone. North of the MCT zone, this velocity increases and reaches ∼3.31 km/s beneath the Tethyan Himalaya. This translates into a velocity reduction of ∼15% and ∼10% of the average shear wave velocity of the underthrust Indian crust, south and north of the MCT zone, respectively. This change in the velocity of the MHT LVL may be indicative of the change in rheology of the MHT from the region of frictionally locked brittle failure to the aseismically creeping zone. The presence of metamorphic fluids (Patro & Harinarayana, 2009) and/or sediments under shear stress in the fault zone and/or reduction in grain size due to repeated brittle failure associated with megathrust earthquakes, over millions of years, can greatly reduce VS within the locked zone. Additionally, brittle failure in fault zone results in lateral heterogeneities which act as scatterers for extrinsic attenuation of the shear wave energy (Thirunavukarasu et al., 2017). In contrast, in the creeping zone, VS is reduced only due to plastic behavior of the materials within the ductile shear zone. The absence of fluids and extrinsic scatterers leads to lesser reduction of VS in creeping zones compared to the locked zone. Our results suggest that the transition to the creeping zone initiates somewhere underneath LCHG and YUMT. This is in agreement with the observed locking line beneath the Sikkim Himalaya (Ader et al., 2012) and coincides with the position of the deeper ramp on the MHT (Figure 7), as observed in the Nepal Himalaya (Elliott et al., 2016).

To first order, the MHT dips gently to the north at ∼9∘. It is first observed at a depth of ∼6–8 km beneath the Lesser Himalaya and deepens to ∼25 km beneath the Tethyan Himalaya. There are observable changes in dip on the MHT, the first one beneath the Lesser Himalaya and the second one beneath the Tethyan Himalaya. This represents a ramp‐flat‐ramp geometry of the MHT, which had also been observed in other parts of the Himalaya (Caldwell et al., 2013; Mitra et al., 2005; Rai et al., 2006). The ramp beneath YUMT is steeper (∼16∘) and is connected to the Lesser Himalayan ramp by a flat (dip ∼5∘). A few LVLs are observed above the MHT within the Lesser and the Higher Himalaya. We conjecture these to be the PT and the MCT which splayed off the MHT. From our 3‐D image of the MHT, we observe a dome structure formed by a combination of ramps beneath the arcuate MCT culmination zone (Figure 7). The dips of the ramps are gentle (∼8∘). The presence of this dome upwarps the overlying structure. The PT and MCT, which appear to originate from the ramps north of this dome structure, are also upwarped.

The doming up of the MHT could result from elevated topography on the underthrusting Indian Plate. In this case, the thickness of the underthrust Indian crust beneath the dome structure should be higher than the surrounding crust, and this is observed from our inverted models. In view of this, we consider the MHT dome to be analogous to a subducting seamount on the top of a downgoing oceanic plate in a subduction system. Upwarping of overlying strata and heterogeneous and complex faulting is observed in the vicinity of seamounts (Dominguez et al., 1998). By a conceptual model, Wang and Bilek (2011) showed that the horizontal tensile stress exerted by a seamount on the upper plate is 1 order of magnitude greater than the normal stress it exerts. Therefore, instead of producing more friction to create large earthquakes, the upper plate crumbles to a network of numerous fractures. This system of failed faults acts as a creep zone, allowing the seamount to propagate with very little or no hindrance resulting in aseismic creeping but can also be associated with microseismicity. As the Indian Plate underthrusts, this dome structure in the Lesser Himalaya creates a network of fractures which may have initiated the active Lesser Himalayan duplex. In the case of the subducting seamount, microseismicity is confined to a region adjacent to the seamount, while the smoother regions are frictionally locked. Similar observations have been made in the regions adjacent to the Lesser Himalayan dome structure. From microseismicity studies in the Sikkim Himalaya (De & Kayal, 2003; Hazarika et al., 2010), we observe that the seismicity is clustered around the region of this dome structure. As we go away from the dome, the frequency of microseismicity decreases. The dome structure may also act like a seamount in stopping rupture propagation when the smooth patch of the neighboring locked zone breaks (Wang & Bilek, 2011). Evidence of such rupture termination of megathrust earthquakes has been seen in the Java subduction zone (Bilek & Engdahl, 2007). The rupture area of the 1934 Bihar‐Nepal earthquake (Mw 8.1) did not propagate eastward of the Nepal‐Sikkim border (Sapkota et al., 2013). The presence of this dome structure underneath Sikkim may provide an explanation for this eastward rupture termination. Fault zones, where some patches rupture and some parts inhibit rupture, are known to produce low stress drops (Brown et al., 2015; Wang & Bilek, 2011). Faulting of the strong segment produces large stress drop but simultaneously increases the stress in the neighboring regions. As a result, the average stress drop is observed to be low. In Sikkim, the stress drop associated with moderate to large earthquakes were found to be low (Paul et al., 2015) supporting the notion of heterogeneous faulting.

4.2 Architecture of the Underthrust Indian Crust and Its Relationship to Transverse Tectonics
The midcrustal discontinuity, within the underthrust Indian Plate, is consistently observed beneath the Sikkim Himalaya. This interface has a first‐order dip to the north and also displays lateral heterogeneity in the form of steep dips (beneath RABN and CHTG), southward dip (beneath GTOK), and imbrication (beneath CHTG). The thickness of the lower Indian crust (between the midcrustal layer and the Moho) lies between ∼14 and 25 km. The average VS of the lower crust decreases from ∼3.8 km/s to ∼3.7 km/s as we go northward from the Lesser Himalaya to the Higher Himalaya. A similar observation has been made in the Uttaranchal Himalaya by Caldwell et al. (2009), which they ascribed to the presence of aqueous fluids/partial melts in the lower crust. We observe oblique LVLs beneath the Higher Himalaya and identify them as transverse structures (faults) (Paul et al., 2015). These low‐velocity transverse structures may provide an alternative explanation for the reduction in velocity. Such structures can also facilitate the propagation of fluids/melts from the lower crust. The average VS of the underthrust Indian Plate lies between ∼3.60 km/s and ∼3.65 km/s, and its average VP/VS is <1.74, consistent with a felsic composition. However, the average VS of the lower crust suggests that it is slightly more mafic and is possibly composed of dry granulites. The uppermost mantle (Sn) velocity lies between ∼4.15 and ∼4.27 km/s, which is slightly lower than the observed Sn velocity beneath the Indian Shield (Mitra et al., 2006). The thickness of the underthrust Indian Plate (between MHT and Moho) varies between 35 km and 42 km, which is consistent with the average thickness of the Indian Shield crust south of the Himalaya.

Similar to the MHT, the Moho also dips gently to the north at an angle of ∼7∘. However, there are a number of second‐order lateral variations on the Moho (Figure 8) in the form of dome structures and deeper sections. These are explained either by imbrication of the lower boundary of an elastic layer under flexure (Figure 6) or by transverse faulting through the lower Indian crust. Paul et al. (2015) studied the source mechanisms of lower crustal earthquakes beneath the Sikkim Himalaya and demonstrated that the underthrust Indian crust deforms by strike‐slip motion on a set of transverse structures. Such transverse structures in the lower crust of the Indian Plate are also observed in our CCP stacks (Figure 6). These structures trend NW‐SE and intersect the entire lower crust at regular intervals (Figure 8). The 2011 Sikkim earthquake, its deeper aftershocks, and previous strike‐slip earthquakes (Figure 8), in southern Tibet immediately north of our study region, occurred close to the Moho and ruptured the base of the seismogenic Indian lower crust. The dextral strike‐slip motion associated with this faulting displaces the eastern block of the lower crust southward relative to the western block. This results in the juxtaposition of a deeper segment of the Moho to the east with a shallower segment of the Moho to the west across the fault. The observed undulations on the Moho underneath the Lesser Himalaya reflect Moho offsets accumulated over several such dextral strike‐slip earthquakes (similar to the Mw 6.9 2011 Sikkim earthquake) on a set of transverse structures present within the underthrust Indian crust beneath the Sikkim Himalaya. The source mechanisms of historical earthquakes, the 2011 Sikkim mainshock, and its deeper aftershocks (Figure 8) reveal that these occurred near the edges of these dome structures. These active transverse structures, along with the distribution of earthquakes, highlight that the lower Indian crust beneath the Sikkim Himalaya is seismogenic (Acton et al., 2011; Mitra et al., 2005). The presence of these active transverse structures should be included in kinematic models of active deformation of the Eastern Himalayan plate boundary system.

A comparison of the results from the Sikkim Himalaya has been made with the adjacent Nepal Himalaya (Nábělek et al., 2009; Schulte‐Pelkum et al., 2005) and the Bhutan Himalaya (Singer et al., 2017). The geometry of the Himalayan detachment (MHT) beneath the eastern Nepal Himalaya (Schulte‐Pelkum et al., 2005) has a gentle northward dip, unlike the ramp‐flat‐ramp geometry observed beneath Sikkim. Farther west beneath the central Nepal Himalaya (Nábělek et al., 2009), the gentle north dipping MHT has been observed to display changes in dip at two points, the first below the Lesser Himalaya and the second below the Higher to Tethyan Himalaya. These are similar to the 2‐D variation observed on the MHT beneath the Sikkim Himalaya. The thickness of the underthrust Indian crust beneath the Nepal Himalaya is comparable to the Sikkim Himalaya, but the geometry of the Moho is relatively smooth and dips to the N‐NE. Beneath the Bhutan Himalaya (east of Sikkim) (Singer et al., 2017), the MHT and Moho have lateral variation from the west to the east, similar to Sikkim. A significant difference in results lies beneath the western Bhutan, where the Moho reveals a steep dip south of the Higher Himalaya and reaches a depth of ∼70 km. The MHT, too, has a moderate change in dip beneath the Lesser to Higher Himalaya and appears as an eastward continuation of the ramp observed beneath the Sikkim Himalaya.

5 Conclusions
We study the 3‐D architecture of the crust beneath the Sikkim Himalaya using receiver function analysis and joint inversion of receiver function and Rayleigh wave group velocity dispersion data. The Indian Plate underthrusts the Sikkim Himalaya with its top (MHT) highlighted by a LVL and its base (Moho) by a large impedance contrast boundary observed in receiver functions from all the stations. To first order, all the crustal discontinuities—the MHT, the midcrust, and the Moho dip northward, at ∼9∘, ∼10∘, and ∼7∘, respectively. From detailed images, we observe that the MHT has a ramp‐flat‐ramp geometry beneath the Lesser and Tethyan Himalaya in Sikkim. The Lesser Himalayan ramp forms a dome structure on the MHT. This upwarps the overlying PT and MCT to form an arcuate geometry observed in its outcrop. This dome geometry on the MHT is a result of elevated topography on the underthrust Indian Plate and is analogous to subducting seamounts. Such a dome structure has the potential to terminate rupture propagation of megathrust earthquakes and result in low stress drops. MHT LVL has a reduction of VS by 15% and 10% beneath the Lesser Himalaya and the Tethyan Himalaya, respectively. This northward increase in VS within the LVL possibly marks the transition from frictionally locked brittle regime to freely sliding aseismic creep regime.

The average VS of the entire Indian crust is ∼3.63 km/s, and its VP/VS is ∼1.72 ± 0.02 which indicates a felsic crustal composition. The average VS of the upper crust increases marginally from south to north, while that of the lower crust decreases northward. We conjecture that this decrease in VS of the lower crust is either due to the variation in the crustal structure of the underthrust Indian Plate or due to the presence of active transverse structures beneath the Higher Himalaya. The average crustal thickness of the underthrust Indian crust varies between 35 km and 42 km and is consistent with the average thickness of the Indian Shield crust south of the Himalaya. The midcrustal discontinuity displays lateral heterogeneity in the form of steep, southward dip, and imbrications. The Moho has second‐order lateral variations in the form of dome structures and undulations. These result from imbrication of the lower boundary of an elastic layer under flexure and/or active transverse faulting in the lower crust.

importance of mathematics in architecture

Can architecture be done without math?
In summary, no. Buildings without sound mathematical underpinnings are a recipe for disaster, which is why math is not an optional extra for architect students. The good news, however, is that you don’t need to be a total math whizz; high-school level competence will do, since computer software does most of the legwork these days. You just have to give it the correct instructions on what to calculate.

In the beginning of architecture, there was geometry.

Architects have been using math since the very start of their field. The earliest known examples of architecture date back to the fourth millennium BC and the ancient Egyptians. They used simple concepts like geometry and arithmetic to help them build simple structures like boats, tombs, and pyramids.

As architecture progressed, math became more advanced and accurate. In ancient Greece, mathematicians like Pythagoras and Euclid developed new concepts that helped architects create more complex structures, including the Parthenon.

The Renaissance brought new innovations in mathematics including calculus and mechanics that allowed for even more complex building designs. Architects like Michelangelo used these ideas in their work when creating places such as the Sistine Chapel ceiling.

Modern architecture has continued to use math throughout its existence. Today’s architects still rely on basic arithmetic and geometry as well as more advanced mathematical principles such as trigonometry or calculus when designing new buildings or planning renovations on existing ones.”

Math forges the foundations of buildings

Every building you spend time in––schools, libraries, houses, apartment complexes, movie theaters, and even your favorite ice cream shop––is the product of mathematical principles applied to design and construction. Have you ever wondered how building professionals incorporate math to create the common structures you walk in and out of every day?

Before construction workers can build a habitable structure, an architect has to design it. Geometry, algebra, and trigonometry all play a crucial role in architectural design. Architects apply these math forms to plan their blueprints or initial sketch designs. They also calculate the probability of issues the construction team could run into as they bring the design vision to life in three dimensions.

Since ancient times, architects have used geometric principles to plan the shapes and spatial forms of buildings. In 300 B.C., the Greek mathematician Euclid defined a mathematical law of nature called the Golden Ratio. For more than two thousand years, architects have used this formula to design proportions in buildings that look pleasing to the human eye and feel balanced. It is also known as the Golden Constant because it manifests literally everywhere.

The Golden Ratio still serves as a basic geometric principle in architecture. You could even call it a timeless archetype, as it evokes in human beings a universal sense of harmony when they see or stand in a building designed with this principle. And perhaps not surprisingly, we see the Golden Ratio demonstrated throughout “architectures” of the natural world.

Calculating ratio is essential, as well, when it’s time to construct a building from the architectural blueprints. For example, it’s important to get the proportions right between the height and length of a roof. To do that, building professionals divide the length by the height to get the correct ratio.

The Pythagorean theorem, formulated in the 6th century B.C., has also come into play for centuries to calculate the size and shape of a structure. This theorem enables builders to accurately measure right angles. It states that in a triangle the square of the hypotenuse (the long side opposite the right angle) is equal to the sum of the squares of the other two sides. 

The most remarkable ancient architecture of all may be the pyramids of Egypt, constructed between 2700 B.C. and 1700 B.C. Most of them were built and scaled at about a 51-degree angle. The Egyptians clearly and mysteriously possessed knowledge of geometry, as evidenced by the accuracy of pyramid construction.

In the modern world, builders use math every day to do their work. Construction workers add, subtract, divide, multiply, and work with fractions. They measure the area, volume, length, and width. How much steel do they need for an office building? How much weight in books and furniture will the library floors need to bear? Even building a small single-family home calls for careful calculations of square footage, wall angles, roofs, and room sizes. How many square yards of carpet? How much water do you need to fill up a swimming pool?

Chances are you’re in a building right now. Look around at the walls and windows. Math is everyplace you walk into––work, school, home, or pet store. Imagine that you are an architect. How would you apply math to build a small dwelling?

geometry in architecture

The architectural style known as Art Deco emerged in France before World War I. The movement, which featured rich colors, bold geometric shapes and lavish ornamentation, became popular in the United States in the 1920s. During this time, skyscrapers such as the Chrysler Building were designed with decorative elements that included zigzag patterns and stepped forms.

Art Deco designs played up geometric shapes in many ways. Zigzags were a common motif. Art Deco buildings often featured zigzags on doors and windows, as well as on brickwork and pillars. Step-like forms also were used to break up walls or provide decorative details.

Geometric shapes also were used to create optical illusions on buildings that resembled pyramids or other three-dimensional forms.

Some buildings wear their geometry on their sleeves – the Great Pyramids, or pretty much anything by Frank Gehry for example, but geometry doesn’t usually shout so loudly. It’s the unsung but essential tool that architects use daily, whether they’re designing a bridge or a block of flats, so in this article we’ve decided to shine a light on geometry in architecture.

what does geometry mean in architecture?

Geometry is an ancient branch of mathematics that works with the points, lines, angles and surfaces of 2D and 3D shapes. This is foundational in architecture. Without geometry, we couldn’t be sure that our buildings were safe, and we’d have a much harder time making them look nice. Architectural plans and drawings would communicate very little. In short, an architect can’t do their job unless they’ve grasped some basic geometrical concepts.

What are some examples of geometrical concepts?

You were probably aware of the most basic geometrical concepts – things like right angles and parallel lines – when you were still a child. At high school, geometry may have gotten a little more complicated; maybe you learnt how to use formulae to calculate the area of a 2D shape (e.g. π r² for a circle), the length of their sides (e.g. Pythagoras’ theorem for a triangle), or the volume of a 3D shape (e.g. length x width x height for a cuboid).Of course, things get more complicated again at college/undergraduate level, but architects don’t wander round with that kind of information in their heads! For advanced geometrical calculations, these days we usually turn to computer software.

How was geometry historically used in architecture?

In the past, it was thought that adhering to strict geometric rules was the key to ensuring buildings were as beautiful as possible. In 20 BCE, a Roman architect named Marcus Vitruvius wrote Ten Books on Architecture, in which he explained the ‘ideal’ proportions that a building should have, based on the proportions of the human body.

Fifteen hundred years later, his writings were rediscovered by Renaissance polymaths such as Leonardo da Vinci (who exemplified them in his drawing ‘Vitruvian man’) and Leon Battista Alberti (who wrote his own version of Ten Books on Architecture). 

Some of the principles Alberti developed included always beginning the design of religious buildings with a circle, since this is a ‘perfect’ shape that can only have been created by god, and ensuring that ratios between elements were maintained across the whole of a building. These kinds of ideas lasted for centuries, and some of them are rarely questioned even now.

How do architects use geometry today?

Many historical ‘rules’ about harmonious proportions in architecture still hold good , but they are no longer strictly followed – in fact, subverting them is actively encouraged. (Would Alberti be horrified or delighted by the Guggenheim Bilbao? We’ll never know.) Of course, you have to know the rules before you can break them.

For contemporary architects, geometry is more of a servant than a master. We use it to make sure that our buildings stay standing; that our plans can easily be understood, even by someone on the other side of the world; and that we don’t populate our cities with ugly, imbalanced architecture – in theory, at least.

Another way we see today’s architects use geometry is in the adoption of ‘biomorphic’ geometric forms, which is to say replicating forms found in the natural world. Of course, Vitruvius and his followers were doing this to some extent when they used the proportions of the human body. But modern architects look to animals and plants, too, taking inspiration from the hexagons of honeycomb (as at the Soumaya Museum, Mexico City) or the bubbles on the surface of water (as the National Swimming Centre, Beijing).

Natural geometry includes patterns such as symmetry, spirals, tessellations and fractals. 

How do architects use geometry as a compositional device?

On one hand, geometry limits what architects can actually do – for example, urban buildings tend to be erected perpendicular to the ground, not only because it makes them stable but also because it allows an area to be more densely packed. (When more space is available this rule can be broken, as in most deconstructivist architecture.)

One the other hand, geometry gives architects a toolkit to work with. Shapes can be combined in infinite ways, so architects compose buildings using things like squares and cubes as building blocks. Take the humble triangle, for instance. It is often considered the strongest shape (it has a firm, supporting base and rarely loses its shape) and therefore a good starting point for a design.

It turns up everywhere as the primary compositional element, from the Great Pyramids of Giza to the Eiffel Tower – which is not only triangular in its overall shape, but also made up of smaller iron triangles (see below).

Why is geometry so important in architecture?

Geometry is the foundation of architecture.

Without geometry, architects wouldn’t be able to design the structures that we consider so beautiful and awe-inspiring. It’s what makes it possible for those buildings to stand up, after all! If a building isn’t built correctly—if it doesn’t have solid foundations and a structurally sound layout—then it can collapse and hurt people.

Architecture has existed since humans first started building shelters, so geometry has always been crucial to making sure those shelters were safe and functional. But even in modern times, geometry is important when we’re creating new buildings—or even just structurally improving existing ones. A solid understanding of geometry is essential for anyone who wants to become an architect, as well as other related fields such as engineering or interior design.

When we think of geometry, we tend to think of Euclidean geometry – the principles devised by the Greek mathematician Euclid over 2,000 years ago. It is still essential to learn these, but the most innovative contemporary buildings rely on ‘new geometries’ as well.

For example, projective geometry happens in ‘projected’ rather than Euclidian space (see the first image below for a visual representation of this), while fractal geometry is based on hierarchies found in nature such as those of a nautilus shell, or Romanesco broccoli (see second image below).

In the final section of this article, ‘Examples of geometry in architecture’, you can see some real-life buildings that use both old and new geometries.

Examples of geometry in architecture

1. Virupaksha Temple, Hampi (~C14)

If you’re interested in the idea of fractal architecture, take a closer look at this Hindu temple in the Indian state of Karnataka. The patterns on the gopuram (entrance tower) divide and repeat as they ascend – just as in they do towards the edges of a snowflake or a leaf.

2. Palazzo Rucellai, Florence by Leon Battista Alberti (1446-51)

This Italian palace was designed by our friend Alberti, who wrote a treatise on how geometry should be used in architecture. The building shows that Alberti practiced what he preached – he designed the façade using a grid, with pilasters and entablatures dividing it into harmonious proportions.

3. Rietveld Schröder House, Utrecht by Gerrit Rietveld (1924)

This Dutch house is one of the only examples of De Stijl architecture. It made no attempt to integrate with its environment, and aimed to shock by eliminating walls and rooms altogether, and existing as an open, changeable space. Rietveld designed it using the golden ratio (1:1.618) which occurs frequently in the natural world, and is a key idea within sacred geometry. 

4. Bauhaus School, Dessau by Walter Gropius (1925)

Gropius’ design for the first Bauhaus school in Germany demonstrates the principles that were taught there. The form of a building was to follow its function (which is to say that decoration was out, and clean lines were in), and all man-made products were to be designed around the square, triangle and circle.

5. Melnikov House, Moscow by Konstantin Melnikov (1927-29)

This house by Soviet architect and artist Melnikov, who refused to build in the style demanded by Stalin, is one of the few cylindrical buildings that has stood the test of time. It actually comprises two cylinders, made of bricks in a honeycomb lattice formation, with asymmetrically-organized hexagonal windows. If this sounds a little eccentric, Melnikov’s original plan was to make a house in the shape of an egg.

6. Headquarters of the United Nations, New York by Harrison & Abramovitz (1951)

The UN building is a slab block that was designed using Le Corbusier’s Modulor scale of proportions. The Modulor was based on the height of a man with his arm held above his head, and was meant to bridge the gap between the metric and imperial systems. UNHQ has always divided opinion, but its distinctive form is iconic. 

7. Philips Pavilion, Brussels by Iannis Xanakis (1958)

Le Corbusier was commissioned to design a pavilion for Expo ‘58 but found himself too caught up in his planned city at Chandigarh, India. He handed over the reins for the pavilion to Xanakis, who created an improbable collection of nine hyperbolic paraboloids in concrete. Sadly, Xanakis’ monument to technological progress was demolished the year after it was built.

8. Opera House, Sydney by Jørn Utzon (1973)

The famous ‘sails’ of Utzon’s Opera House are in fact slices of spheres, cast in concrete. Each slice is coated with triangular and diamond-shaped tiles, arranged in a chevron pattern, that are only visible when standing close to the building. Though today curved buildings are more commonplace, the Opera House was bold and startling when it was first unveiled. 

9. CN Tower, Toronto by multiple architects (1976) 

The CN Tower was the world’s tallest tower for over three decades (Guangzhou’s Canton Tower swiped its crown in 2009), a title you don’t win without the help of geometry. The ratio of the observation deck to the tower’s total height is 0.618, taking into account the principle of the golden ratio. 

10. Sagrada Família, Barcelona by Antonio Gaudí (begun 1882, construction ongoing)

Where to begin with this one? Gaudí’s basilica looks like it shouldn’t exist outside the pages of a fairy tale, and yet it does – mostly. The original plan includes three grand facades, 18 spires, and an interior in which no surface is flat, and some of these are now on their way to completion. Thanks to advances in CAD, it is now estimated that the Sagrada Família could be finished by 2026.

Summary

When you think about it, it’s amazing how geometric shapes are used in every aspect of our lives. To build a bridge, for example, you need to know the strength of its arches and the depth of its foundations. A pyramid or a dome is an ideal shape for strength and stability, while the arch is designed to withstand the pressure of stones above it – it’s all about straight lines and angles!

But geometry doesn’t have to be confined to buildings. Where would we be without geometry? Under a pile of rubble, probably! At best, we’d be living and working in buildings that would barely warrant a second thought, never mind pondering in open-mouthed wonder. Understanding geometry helps architects to make towns and cities beautiful, though thankfully today you needn’t be a slave to ‘the rules’. All you really need is a square, a triangle, a circle and a dash of imagination – then the world is your oyster!

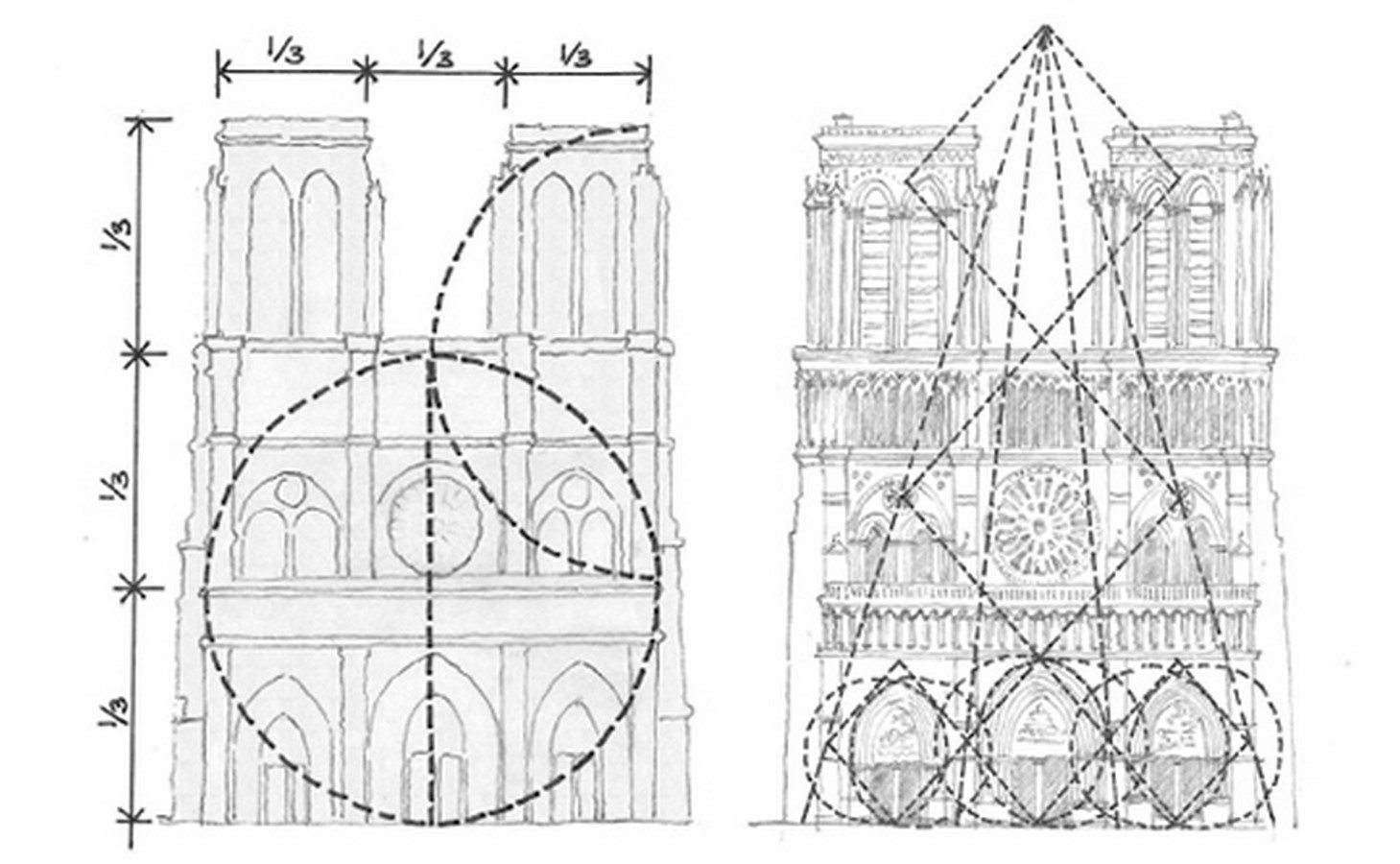
Which geometric shapes are mostly used in architecture?

The number of geometric shapes used regularly in architecture is actually very small. Many are quite impractical when it comes to building – with the exception of triangles, squares / rectangles, and circles.

We already mentioned that the triangle is the ‘strongest’ shape, because it can’t be distorted. A rectangle will become a parallelogram if it’s pushed hard enough, but a triangle always holds its form. That’s why it’s so often used in bridges, roofs and electricity pylons, whose collapse would be disastrous. It also tessellates beautifully, of course.

Squares and rectangles are also practical shapes for architecture. They are easy to construct out of common building materials like metal and concrete; their right angles provide sturdiness and reliability; and they fit together in a straightforward way, reducing cost and waste. It’s also easy to scale a square or rectangle up or down, which is not the case with more complex polygons.

As for circles, you might think they’re rarely used in buildings but that’s not true in reality. Sure, you don’t see them as much, but they’re doing a lot of the legwork in things like domes and arches. They work well in sustainable architecture for a number of reasons (e.g. less material is needed overall; they allow wind to flow more easily around them), and they are nearly as strong as triangles because stress is distributed evenly across the whole shape. However, circles are much harder to work with (imagine cutting a square of wood, then imagine cutting a circle).  

A note on ‘geometric’ and ‘natural’ shapes

It’s a common misconception that geometry only applies to squares, triangles and other shapes that exist in the man-made world. In fact, natural patterns are geometric too.

In everyday life, we often see things as being either regular or irregular. A tree is different from a rectangle; one is organic and one is geometric. But trees have their own pattern, and as it turns out, this pattern has been copied in architecture for a long time. Traditionally, geometric shapes were defined as those that could be constructed using Euclidean geometry: squares, triangles, cones, prisms and so on. These were contrasted with organic forms, which were thought to be complex and irregular. But the new geometries began to make sense of nature’s apparent chaos; we now understand that while a tree is very different from a rectangle, it has its own pattern – and one that has been copied in architecture for a long time. You may find older textbooks that maintain a distinction between geometry and nature, but in many ways they rely on one another.

  

Some people even believe in the idea of ‘sacred geometry’ – that everything in nature, from a leaf to a galaxy, has its own geometric pattern. The problem is just that humans are too dim to understand them all, so we stick to manageable things like rectangles!

Ok, we’ve made it through the most common math formulas used in architecture. You are now armed with all the knowledge you need to take on the world of building. We hope you’re ready for some serious geometry, because architecture is no joke.

To make sure you’re retaining all this information, go back through this article and try to use the formulas in different ways! Do a little online research about famous structures and see if you can identify which formula was needed for that process. If you come up with something cool, let us know—we love hearing from students just like you!

If you want to learn more about math in your future career as an architect, check out our other articles on math topics specifically related to architecture, including “Math Skills Every Architect Needs” and “Why Architects Need To Know Algebra.”

We hope this article has helped you learn how to use math in your architectural journey. And remember—when it comes to studying math in your future career, there’s no such thing as too much practice! If you’re not sure where to start, read this article next: How To Use Math In Architecture: The Basics.